Thread by @brusicor02

Et voilà les résultats du dernier petit problème.
Beaucoup de personnes ont posté leurs raisonnements, et c'était très instructif de voir les présentations de chacun. Je vais faire un rapide corrigé. (1/12)

https://twitter.com/brusicor02/status/1042099658112348163

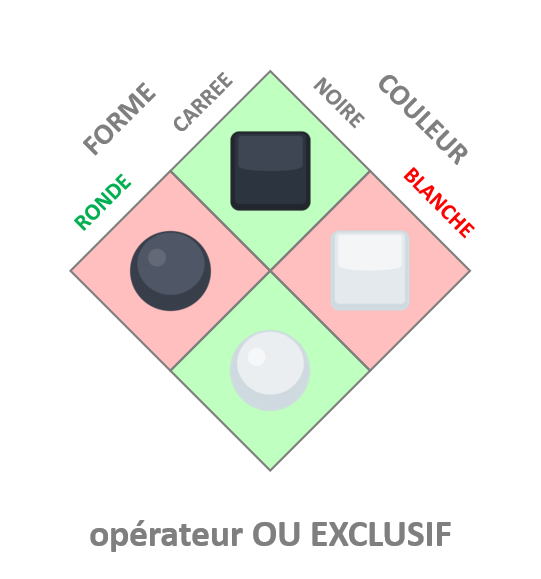
#LT Le piège présent dans l'énoncé, c'est cette formulation avec ce qu'on appelle un "ou exclusif" : une seule des conditions doit être vérifiée, pas les deux en même temps.
Un peu comme le "fromage ou dessert" : vous ne pouvez pas prendre les deux en même temps. (2/12)

#LT Ainsi, si "⚪️ est machin", ça veut dire que SEULEMENT UNE des caractéristiques est vraie :
1⃣ soit c'est la forme ronde qui est la bonne
2⃣ soit c'est la couleur blanche qui est bonne
Je vais développer chacun des cas. (3/12)

#LT Cas 1⃣ : c'est la forme ronde qui fait partie des conditions. L'autre condition est forcément fausse pour ⚪️ : la condition de couleur est donc noire.
Donc qui peut être dit "machin" ?
- ⚪️, qui est rond mais pas noir
- ◼️, qui est noir mais pas rond
(4/12)

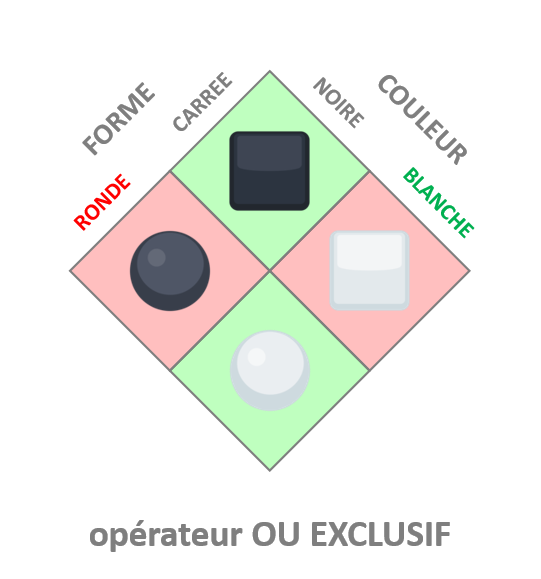
#LT Cas 2⃣ : c'est la couleur blanche qui fait partie des conditions. L'autre condition est forcément fausse pour ⚪️ : la condition de forme est donc carrée.
Donc qui peut être dit "machin" ?
- ⚪️, qui est blanc mais pas carré
- ◼️, qui est carré mais pas blanc
(6/12)

#LT On peut aussi raisonner ainsi :
- si ⚪️ est machin, 1 de ses caractéristiques est vraie et l'autre est fausse
- ◼️ est l'opposé total : ce qui était vrai est devenu faux et ce qui était faux est devenue vrai. Toujours 1 seule caractéristique vraie, ◼️ est machin (7/12)

#LT Mais est-ce que ⬜️ peut être machin ? Non, puisque :
- soit j'ai changé la caractéristique qui était juste, alors j'ai 2 faux
- soit j'ai changé la caractéristique qui était fausse, j'ai alors 2 vrai et ça ne peut donc pas être un machin. (8/12)

#LT Donc la bonne réponse était la deuxième : "◼️ est machin, ◻️ non"
Environ un quart d'entre vous a donné la bonne réponse, ce qui je dois vous avouer était attendu. (9/12)

#LT Le problème que j'ai soumis est en fait une variation du "thog problem" de Peter Wason. Il avait obtenu dans son expérience seulement 10% de bonnes réponses et plusieurs articles décrivent les sources de ces "erreurs intruitives". (10/12)
onlinelibrary.wiley.com/doi/abs/10.111…

#LT Et comme le dit Gérald Bronner dans "La démocratie des crédules", ces problèmes sont sournois car l'intuition semble donner une solution évidente, ce qui est une incitation forte à ne plus y réfléchir ensuite. C'est un biais qu'il nomme "avarice intellectuelle" (11/12)

#LT Conclusion, méfiez-vous des évidences, et n'ayez pas peur de poser calmement le problème avant de répondre précipitamment. Et remerciez votre crétin de cerveau d'avoir autant de biais qui nous fait tomber dans le panneau. 😅
(12/12)