Thread by @MaartenvSmeden

What does one get when mindlessly applying logistic regression to a too small dataset? Well…

[thread]

Just to be clear, I have zero interest in shaming these authors. Small sample logistic regression analyses are very common! But for those of you interested here is the link: journalacs.org/article/S1072-…

“The aim of this study was to evaluate the impact of medical student placement of Foley catheters on rates of postoperative catheter-associated urinary tract infection (CAUTI)”.

The study compared medical student placement to residents and nurses using data from an existing registry. Wouldn’t this be better done using a randomized trial you ask? I’ll leave that to you to judge

By the way: does this study sounds familiar? Could very well be! @ADAlthousePhD flagged some of the issues with this paper only a few days ago

Back to the actual study. The sample size seems rather reasonable with 891 surgical patients. At first. But only 2.4%, meaning ~22 number of events, actually developed CAUTI

So what can go wrong with few events (22) and a bunch of factors (20) that you want to put in a logistic regression model?

Problem 1: there is such limited data that it becomes impossible to meaningfully select important confounders

In general, when interested in correcting for confounding the data itself alone is insufficient to tell you about what is and isn’t an important confounder. If you don’t already, follow @EpiEllie for great tweetorials about causal inference by observational data

The worst one can do is so-called “univariable screening”. More details about the possible harms of univariable screening are found here: doi.org/10.1016/0895-4…. For some reasonable suggestions for selecting among candidate confounders, check: academic.oup.com/aje/article/16…

Problem 2: small sample bias (a.k.a. sparse data bias) needs attention in data with low number of events

Perhaps a less known property of logistic regression is that its parameters are *biased* towards more extreme values in data with few events. This bias can be rather large (>50%) when the number of events becomes close to the number of confounders approaches the number of events

Consequently, the odds ratio’s estimated from logistic regression with few events are simply too high. For more details, read: dx.doi.org/10.1136/bmj.i1…

Problem 3: (near) separation is likely in data with lower number of events

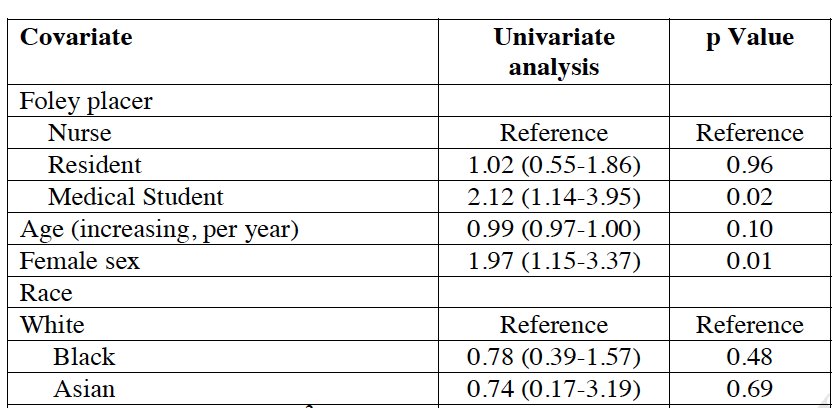
High regression coefficient values combined with high estimated standard errors are a telling sign of separation. The "CAUTI study" has a great example of such a sign, also look at the upper bound of the confidence interval for the odds ratio. 693?

For #rstats users, consider this toy example:

require(rms)
require(logistf)

set.seed(2018)
x <- rnorm(100)
y <- ifelse(x<0,0,1)
summary(glm(y~x,family="binomial"))
logistf(y~x,firth=F)

The code analyses the same data (subject to separation) with identical logistic regression models, just different functions. The results (log-odds ratio for factor x) may be surprising:

Model 1: log(OR) = 1478 , p = 0.990
Model 2: log(OR) = 111, p = 0.000

To be clear: two analyses on the same data, the same model, the same software program, just different functions producing widely different results!

Which function is right? Both of them did EXACTLY what we asked them to do. Unfortunately, we asked them to solve an unsolvable problem. That is, unsolvable under the standard maximum likelihood estimation paradigm. Read more about separation here: ncbi.nlm.nih.gov/pubmed/29020135

The CAUTI study is a textbook example suffering from all 3 aforementioned problems. Can we solves these problems? To some extent: yes, using more clever statistical analysis techniques! Should we? Well… probably not

Because the fourth problem we can’t solve is lack of precision. With 22 events observed and 20 factors in the model there is simply no way to get sufficiently precise estimates of effect to become even slightly informative

Look at the effect of primary interest has a confidence interval ranging between 1.2 to 13.7. Still ignoring the three earlier problems and possibly residual confounding, which in when taken into account would further widen the confidence interval and lower the point estimate

So is there any back-up for the conclusion of the CAUTI study to support their assertion that more intense supervision of medical students is need because the associated odds are 4 times as high? Obviously not

As uncomfortable as it may sound, very often the best advice for a planned study with insufficient data / sample size is to not do the study at all

[end thread]